Optimisation linéaire
Optimisation linéaire
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Ce cours d'optimisation linéaire est destiné à des étudiants en Mathématiques apliquées ou Informatique, niveau troisième année universitaire. Il est basé essentiellement sur la référence ci-après :
:
Hédi Nabli, ''Recherche Opérationnelle : Algorithme du Simplexe et ses Applications'', Centre de Publication Universitaire, Tunisie (2006)
Ce livre propose entre autres
- une nouvelle méthode de recherche d'une base réalisable initiale pour l'algorithme du simplexe. Cette technique ne fait pas intervenir les variables artificielles. De plus il est souvent possible d'aboutir, en une seule itération, à une base réalisable.
- Grâce aux tableaux formels, une nouvelle alternative, autre que l'algorithme dual-simplexe, est proposée.
- Pour les problèmes de transport, un algorithme récursif pour la détermination des éléments d'un tableau de transport est mis en oeuvre.
Dans ce document, les résultats mathématiques sont donnés sans démonstration. Pour plus de détails, on peut consulter la référence ci-dessus.
V Algorithme du simplexe standard
VI Dualité en programmation linéaire
Vous trouverez ici une version pdf : docquadratic.pdf
Je remercie vivement Sophie Lemaire et Bernadette Perrin-Riou, enseignants-chercheurs à l'université de Paris-Sud, pour leur aide précieuse à réaliser ce document interactif.
I Programmation linéaire
Optimisation linéaire
→ I Programmation linéaire
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Un programme linéaire est un problème dans lequel on est amené à maximiser (ou minimiser) une application linéaire, appelée fonction d'objectif ou fonction économique, sur un ensemble d'équations et/ou d'inéquations linéaires, dites contraintes. Autrement dit, la programmation linéaire est une branche des mathématiques qui a pour but de résoudre des problèmes d'optimisation linéaire de type
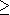 ''. En multipliant chaque inégalité de type ''
''. En multipliant chaque inégalité de type ''
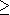 '' par
, on peut supposer que toutes les contraintes d'inégalité
sont de type ''
'' par
, on peut supposer que toutes les contraintes d'inégalité
sont de type ''
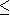 ''.
''.
Optimisation linéaire
→ I Programmation linéaire
I-1 Généralités
Optimisation linéaire
→
I Programmation linéaire
→ I-1 Généralités
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Dans le contexte de la programmation linéaire, le terme programmation désigne l'organisation des calculs et non la réalisation d'un programme informatique. Du point de vue des applications, l'optimisation linéaire est d'une grande portée. Elle s'applique à des problèmes très variés qui sont issus de l'économie, de l'ingénierie, de la physique ou encore des modèles probabilistes. Dans ce cadre, on peut citer par exemple, les problèmes de type gestion de stock, gestion de production, transport de marchandise, affectation du personnel, systèmes industriels, réseaux de communication, etc. Pour les modèles de programmation linéaire, on est souvent amené à maximiser un gain ou minimiser un coût. Ceci explique d'ailleurs pourquoi la fonction à maximiser s'appelle fonction d'objectif ou économique.
Optimisation linéaire
→
I Programmation linéaire
→ I-1 Généralités
I-2 Exemple
Optimisation linéaire
→
I Programmation linéaire
→ I-2 Exemple
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Exemple
Une usine fabrique deux produits (A) et (B) à
l'aide des matières premières I, II et III. Le fonctionnement
de l'usine est comme suit :
- unité du produit (A) nécessite unités de I et unité de II.
- unité du produit (B) nécessite unité de I, unités de II et unité de III.
Formulation mathématique
Si on désigne respectivement par
et
les
quantités vendues du produit (A) et (B), le gain total vaut
D'autre part, la disponibilité en matières premières revient
à exiger des quantités, utilisées pour la
fabrication de
et
, qui soient inférieures aux
quantités disponibles. Ces contraintes s'expriment par les inégalités
suivantes :
Bien entendu, les variables
et
doivent être
positives. En conclusion, le problème de maximisation du profit
se traduit mathématiquement par un programme linéaire qui
s'écrit sous la forme :
Optimisation linéaire
→
I Programmation linéaire
→ I-2 Exemple
I-3 Domaine réalisable
Optimisation linéaire
→
I Programmation linéaire
→ I-3 Domaine réalisable
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Pour un problème d'optimisation linéaire, tout point qui vérifie l'ensemble des contraintes s'appelle point réalisable ou admissible. L'ensemble de tous les points réalisables s'appelle domaine réalisable. Il est facile de vérifier que le domaine réalisable d'un programme linéaire est convexe. On rappelle qu'un ensemble est dit convexe si à chaque fois qu'il contient deux points et , il contient le segment joignant et . Ce segment est souvent noté par et il est défini par
Optimisation linéaire
→
I Programmation linéaire
→ I-3 Domaine réalisable
I-4 Présentation des méthodes
Optimisation linéaire
→
I Programmation linéaire
→ I-4 Présentation des méthodes
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Nous allons présenter des techniques qui permettent de résoudre les programmes linéaires que l'on convient désormais de noter (PL). Diverses méthodes ont été proposées dans la littérature :
- La méthode graphique : l'utilisation de cette méthode est restreinte aux (PL) ayant un nombre de variables au plus égal à .
- La méthode des sommets : le nombre de sommets étant prohibitif, cette méthode est très coûteuse en temps de calcul.
- La méthode du simplexe : algorithme itératif mis au point par George Dantzig en 1951.
Optimisation linéaire
→
I Programmation linéaire
→ I-4 Présentation des méthodes
II Méthode graphique
Optimisation linéaire
→ II Méthode graphique
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Nous allons décrire la méthode graphique à travers trois exemples représentatifs, ayant chacun deux variables structurelles. Le premier admet une et une seule solution optimale. Le deuxième admet une infinité de solutions optimales. Par contre, le troisième exemple n'admet aucune solution optimale.
La résolution d'un (PL) par la méthode graphique se fait selon une démarche commune, celle-ci peut être résumée en quatre directives :
- Schématiser le domaine réalisable dans un repère orthonormé.
- Dans le même repère, représenter l'hyperplan . Noter que tout hyperplan d'équation , , est parallèle à .
- Si le (PL) considéré est de type maximisation ( resp. minimisation), indiquer, par une flèche, le sens de déplacement parallèle de qui fait augmenter ( resp. diminuer) .
- Déterminer la droite la plus éloignée (dans le sens de la flèche) de et qui coupe le domaine réalisable . Tout point de est une solution optimale. Si une telle droite n'existe pas, cela veut dire que l'optimum est infini.
Optimisation linéaire
→ II Méthode graphique
II-1 Exemple 1
Optimisation linéaire
→
II Méthode graphique
→ II-1 Exemple 1
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Reprenons l'exemple
 |
| Représentation graphique pour l'exemple 1 |
Le domaine réalisable est schématisé en gris sur la Figure. Toute droite d'équation , où est un réel fixé, est parallèle à la droite : . On constate aussi que tout déplacement parallèle de dans le sens de la flèche (voir dessin ci-après) fait augmenter . Donc maximiser la fonction , tout en satisfaisant aux contraintes du problème, revient à chercher la droite la plus éloignée (dans le sens de la flèche) de et qui coupe le domaine réalisable. Du point de vue graphique, il s'agit de la droite passant par le point et parallèle à . Ainsi, on peut conclure que le point est la seule solution optimale qui donne une valeur maximale de la fonction d'objectif égale à . Autrement dit, le meilleur profit vaut DT obtenu en fabriquant unités du produit (A) et unités du produit (B).
Optimisation linéaire
→
II Méthode graphique
→ II-1 Exemple 1
II-2 Exemple 2
Optimisation linéaire
→
II Méthode graphique
→ II-2 Exemple 2
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
On considère le (PL) suivant :
 |
| Représentation graphique pour l'Exemple 2 |
Le domaine réalisable est la partie non bornée représentée partiellement en gris sur la Figure. Tout déplacement parallèle de dans le sens de la flèche (voir dessin ci-après) fait augmenter . Donc tout point de la demi-droite est optimal et la valeur maximale de vaut (voir dessin ci-après).
Optimisation linéaire
→
II Méthode graphique
→ II-2 Exemple 2
II-3 Exemple 3
Optimisation linéaire
→
II Méthode graphique
→ II-3 Exemple 3
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
On considère maintenant le (PL) suivant :
 |
| Représentation graphique pour l'Exemple 3 |
Le domaine réalisable associé à ce (PL) est la partie non bornée représentée partiellement en gris dans la Figure. Dans le graphique, on observe que toute droite d'équation , avec , coupe le domaine réalisable. Donc, et par conséquent, le problème n'admet aucune solution optimale (voir dessin ci-dessous).
Optimisation linéaire
→
II Méthode graphique
→ II-3 Exemple 3
II-4 Remarque
Optimisation linéaire
→
II Méthode graphique
→ II-4 Remarque
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Tous les exemples traités ci-dessus possèdent deux
variables structurelles
et
. Pour des (PL) en dimension
, le raisonnement pour la méthode graphique reste le même.
La seule différence est que l'ensemble des points
vérifiant une contrainte
se représente par un demi-espace
qui est délimité par le plan d'équation
Optimisation linéaire
→
II Méthode graphique
→ II-4 Remarque
II-5 Exercice
Optimisation linéaire
→
II Méthode graphique
→ II-5 Exercice
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Exercice
A venir
Optimisation linéaire
→
II Méthode graphique
→ II-5 Exercice
III Méthode des sommets
Optimisation linéaire
→ III Méthode des sommets
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
La méthode des sommetsest simple, elle se base sur la résolution des systèmes linéaires de Cramer. Cependant, elle est dans la pratique inexploitable car le nombre de systèmes à résoudre est en général trop important.
Néanmoins, la méthode des sommets est d'une utilité incontestable : la recherche de l'optimum éventuel sur tout le domaine réalisable se ramène au calcul de l'optimum de la fonction d'objectif restreinte à un sous ensemble fini. Ce résultat sera l'un des outils clé de la méthode du simplexe.
Définition
Optimisation linéaire
→ III Méthode des sommets
III-1 Résultat préliminaire
Optimisation linéaire
→
III Méthode des sommets
→ III-1 Résultat préliminaire
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Considérons un (PL) à variables réelles. Un point du domaine réalisable est appelé sommet, s'il existe hyperplans frontières dont l'intersection est réduite à .
Théorème
Soit
une application linéaire et
un polyèdre de
. Si
admet son optimum
global en un point de
, il est
aussi atteint en un sommet de
.
Sans nul doute, l'intérêt de ce théorème est immédiat :
L'optimum (que ce soit maximum ou minimum) d'un
(PL), lorsqu'il existe, peut toujours être réalisé sur un
sommet.
La méthode des sommets pour la résolution d'un (PL), consiste donc à :
- déterminer tous les sommets du domaine réalisable,
- puis calculer la valeur de en chacun de ces sommets.
Exercice
Application 1 : Problème de trains
Exercice
Application 2 : Production optimale
Optimisation linéaire
→
III Méthode des sommets
→ III-1 Résultat préliminaire
III-2 Mise en oeuvre
Optimisation linéaire
→
III Méthode des sommets
→ III-2 Mise en oeuvre
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Appliquons la méthode des sommets aux trois exemples précédents. Pour l'exemple , les sommets du domaine réalisable sont les points (voir Figure )
Exercice
Méthode graphique générale
Optimisation linéaire
→
III Méthode des sommets
→ III-2 Mise en oeuvre
III-3 Champ d'application
Optimisation linéaire
→
III Méthode des sommets
→ III-3 Champ d'application
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
La méthode des sommets peut s'appliquer même pour des (PL) ayant un nombre de variables structurelles strictement supérieur à . Afin de déterminer un sommet, on choisit hyperplans ( étant le nombre de variables) parmi les contraintes du domaine réalisable (y compris les contraintes de positivité : ). On obtient ainsi un système linéaire d'ordre que l'on résoud. Si ce système admet une et une seule solution , on vérifie si satisfait les contraintes restantes. Dans ce cas, est un sommet, sinon le choix considéré de ces équations linéaires ne permet pas d'avoir un sommet et pour ce faire, on effectue un autre choix de hyperplans frontières parmi les contraintes. Dans le but d'obtenir tous les sommets, il va falloir balayer tous les choix possibles dont le nombre est égal à . Chaque choix qui aboutit à un système de Cramer dont la solution est réalisable permet d'obtenir un sommet. Enfin, la solution du problème considéré est obtenue en prenant l'optimum de la fonction d'objectif sur tous les sommets.
Remarque
Dans la pratique, la méthode des sommets est en fait très
coûteuse en temps de calcul. D'une part, la détermination
d'un sommet exige la résolution d'un système linéaire de
Cramer d'ordre
dont la solution doit satisfaire les
contraintes restantes. D'autre part, le nombre
est en
général très important. A titre indicatif, on a
! Par ailleurs, cette méthode n'est
applicable que lorsqu'on
est certain que le (PL) admet une solution optimale, ce
qui est a priori difficile à vérifier.
Exercice
Résolution par la méthode des sommets : A venir
Optimisation linéaire
→
III Méthode des sommets
→ III-3 Champ d'application
IV Méthode du simplexe
Optimisation linéaire
→ IV Méthode du simplexe
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Dans ce chapitre, nous allons étudier une méthode qui évite de parcourir tous les sommets. Plus précisément, le passage d'un sommet à un autre se fait en améliorant la valeur de la fonction à optimiser. De plus, elle fournit un test qui permet d'affirmer le cas échéant que le problème n'admette pas de solution. Nous verrons que les résultats concernant les problèmes de type maximisation, comparés à ceux relatifs aux problèmes de minimisation, sont très similaires.
IV-3 Relation entre la frome canonique et standard
Optimisation linéaire
→ IV Méthode du simplexe
IV-1 Forme canonique
Optimisation linéaire
→
IV Méthode du simplexe
→ IV-1 Forme canonique
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
On convient de dire qu'un vecteur est inférieur à un vecteur , et on écrit , si pour tout , on a . Ici, le terme désigne la -ième composante du vecteur . Nous mettons en garde sur le fait que
la négation de n'est pas .
En effet, l'inégalité traduit la propriété pour toute composante . Par contre, la négation de , que l'on convient de noter , exprime que l'inégalité ait lieu pour au moins une composante .
Définition
Une forme canonique ( resp.
forme standard)
est un (PL) où toutes les
contraintes sont des inégalités ( resp. égalités) et les variables
sont astreintes à être positives.
On a déjà expliqué qu'on peut supposer et sans perte de généralité, que les contraintes d'inégalité sont toutes de type ''
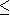 ''. Par
conséquent, on peut affirmer que tout (PL) sous forme canonique
s'écrit sous la forme suivante :
''. Par
conséquent, on peut affirmer que tout (PL) sous forme canonique
s'écrit sous la forme suivante :
Le vecteur a composantes réelles et désigne l'opérateur transposé. Les inégalités
Optimisation linéaire
→
IV Méthode du simplexe
→ IV-1 Forme canonique
IV-2 Forme standard
Optimisation linéaire
→
IV Méthode du simplexe
→ IV-2 Forme standard
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
La mise sous forme standard d'un (PL) quelconque consiste à transformer les contraintes d'inégalités (mise à part les contraintes de positivité) en égalité tout en imposant aux variables d'être positives. Pour ce faire, on procède comme suit :
- A chaque contrainte de type ''
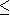 '' (resp. ''
'' (resp. ''
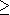 ''),
ajouter (resp. retrancher) une variable tout en lui imposant
d'être positive. Celle-ci s'appelle variable d'écart.
''),
ajouter (resp. retrancher) une variable tout en lui imposant
d'être positive. Celle-ci s'appelle variable d'écart.
- Remplacer chaque variable sans restriction de signe par la différence de deux variables positives : avec et .
- Si une variable est négative, effectuer le changement de variable .
Soit la forme canonique (FC) suivante :
max
sous les contraintes
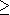
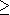
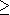 0,
0,
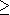 0
0
sous les contraintes
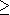
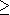
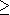 0,
0,
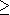 0
0
Les données de la forme standard de cette (FC) sont :
,
=
=
Exemple
On peut dire à juste titre que ce (PL) n'est pas une forme canonique car la première contrainte est une égalité et la troisième variable n'est pas astreinte à être positive. Pour la mise sous forme standard, la première contrainte, qui est déjà une égalité, reste inchangée. Pour la deuxième, on lui retranche une variable positive , elle devient
Optimisation linéaire
→
IV Méthode du simplexe
→ IV-2 Forme standard
IV-3 Relation entre la frome canonique et standard
Optimisation linéaire
→
IV Méthode du simplexe
→ IV-3 Relation entre la frome canonique et standard
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
L'écriture d'un (PL) sous forme standard est introduite tout simplement parce que l'algorithme du simplexe ne s'applique qu'aux formes standards. En d'autres termes,
pour résoudre un (PL) par le simplexe, il faut tout d'abord l'écrire sous forme standard.
Etant donné qu'on résoud le (PL) proprement dit et non la forme standard associée, la question naturelle qu'on se pose est de savoir comment retrouver une solution optimale du (PL) de départ à partir d'une solution optimale de sa forme standard. Le théorème suivant établit le lien entre une solution optimale d'un (PL) et celle de sa forme standard, et on se limite au cas où le (PL) considéré est une (FC).
Théorème
est une solution optimale de (FC) si et seulement si
est une solution optimale de la forme
standard associée. De plus, on a
Ce théorème se généralise bien évidemment pour tout (PL) quelque soit son type d'écriture. A titre d'illustration, pour l'Exemple qui n'est pas sous forme canonique, si est une solution optimale de la forme standard associée, compte tenu des variables d'écarts et du changement de variable considérés, on peut dire que est une solution optimale du (PL) initial.
Exercice
Forme standard : à venir
Optimisation linéaire
→
IV Méthode du simplexe
→ IV-3 Relation entre la frome canonique et standard
IV-4 Notion de base réalisable
Optimisation linéaire
→
IV Méthode du simplexe
→ IV-4 Notion de base réalisable
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Désormais, on note tout (PL) écrit sous forme standard par (FS). Par définition, l'écriture matricielle d'un problème (FS) possède la forme suivante :
sont fixés.
La matrice
contient toujours plus de colonnes que de lignes
(i.e.
) vu que le nombre de variables
structurelles
(variables de décision + variables d'écarts
+ variables dûes aux variables sans restriction
de signe) dépasse le nombre de contraintes
. Sans perte de
généralité, on suppose que la matrice
est de rang
. Sinon,
- ou bien il y a une (ou plusieurs) équation qui est combinaison linéaire des autres équations, qu'il faut alors enlever,
- ou bien le système est incompatible et dans ce cas le système linéaire n'admet aucune solution.
Optimisation linéaire
→
IV Méthode du simplexe
→ IV-4 Notion de base réalisable
IV-4-1 Système de base
Optimisation linéaire
→
IV Méthode du simplexe
→
IV-4 Notion de base réalisable
→ IV-4-1 Système de base
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Notons par la colonne de . Le vecteur colonne s'écrit alors
une base du problème (FS) n'est autre qu'une sous matrice carrée de d'ordre et inversible.
Pour mieux visualiser une telle base , on effectue des permutations de colonnes de sorte que la base apparaisse sur les premières colonnes de . Ainsi, on met sous la forme suivante :
Les variables , , peuvent aussi être classées selon et :
Noter que toute solution de base réalisable admet composantes nulles relatives aux variables hors base et que les autres composantes vérifient un système de Cramer d'ordre .
Optimisation linéaire
→
IV Méthode du simplexe
→
IV-4 Notion de base réalisable
→ IV-4-1 Système de base
IV-4-2 Optimalité et base réalisable
Optimisation linéaire
→
IV Méthode du simplexe
→
IV-4 Notion de base réalisable
→ IV-4-2 Optimalité et base réalisable
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Par analogie au Théorème , nous allons établir que lorsque (FS) admet une solution, on peut toujours chercher une solution optimale parmi les solutions de base réalisable.
Théorème
Si un problème (FS) admet un optimum global, il existe toujours une
solution optimale qui est une solution de base réalisable.
Remarque
Tout sommet du
domaine réalisable
est une
solution de base réalisable, la réciproque est également vraie. Les sommets
de
correspondent donc aux solutions de base réalisable. De
ce fait, l'algorithme du simplexe ne s'intéresse qu'aux solutions
de type
avec
. Ces solutions de base réalisable sont bien évidemment en nombre fini.
Optimisation linéaire
→
IV Méthode du simplexe
→
IV-4 Notion de base réalisable
→ IV-4-2 Optimalité et base réalisable
IV-4-3 Base dégénérée
Optimisation linéaire
→
IV Méthode du simplexe
→
IV-4 Notion de base réalisable
→ IV-4-3 Base dégénérée
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Une solution de base réalisable est dite dégénérée, si en plus des composantes nulles relatives à , il existe une composante du vecteur qui est nulle. Elle est non dégénérée dans le cas où toutes les composantes de sont non nulles et par suite strictement positives. De même, on dit qu'une base réalisable est dégénérée si la solution de base associée est dégénérée. Il est intéressant de noter qu'un point dégénéré est solution de plusieurs bases réalisables. En effet, tout vecteur colonne relatif à une base dégénérée admet au moins une coordonnée , , qui est nulle. En considérant que , on obtient
Optimisation linéaire
→
IV Méthode du simplexe
→
IV-4 Notion de base réalisable
→ IV-4-3 Base dégénérée
IV-5 Algorithme du simplexe
Optimisation linéaire
→
IV Méthode du simplexe
→ IV-5 Algorithme du simplexe
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
L'algorithme du simplexe est un procédé itératif qui progresse dans un sens évolutif : il passe d'une solution de base réalisable non optimale à une autre solution ayant une meilleure valeur d'objectif. De cette façon, on évite de parcourir toutes les solutions de base réalisable dont le nombre est en général prohibitif. Pour vérifier la non optimalité d'une solution, un simple test sera effectué. De plus, grâce à l'algorithme du simplexe, on sera capable de détecter, le cas échéant, que l'optimum est infini.
Optimisation linéaire
→
IV Méthode du simplexe
→ IV-5 Algorithme du simplexe
IV-5-1 Condition d'optimalité
Optimisation linéaire
→
IV Méthode du simplexe
→
IV-5 Algorithme du simplexe
→ IV-5-1 Condition d'optimalité
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
La fonction d'objectif est entièrement définie par la donnée du vecteur . A chaque base , on note et . D'une façon équivalente, le vecteur (resp. ) s'obtient à partir de en prenant les coordonnée relatives aux variables de base (resp. hors base) associée à la matrice (resp. ). Le classement du vecteur selon et donne . Naturellement, on dit qu'une base est optimale si la solution associée est optimale.
Théorème
On se donne une base réalisable
du problème (FS). Si la
forme standard (FS) est de type maximisation (resp.
minimisation), on considère le vecteur ligne
(resp.
). Alors, on a :
- (i) est optimale.
- (ii) Si de plus la base est non dégénérée (i.e. ), alors
La condition d'optimalité peut être interprétée comme un test d'arrêt des itérations pour l'algorithme du simplexe. Il reste à décrire la technique qui permet de passer d'une solution de base réalisable non optimale à une autre solution de base réalisable ayant une meilleure valeur économique. Cette partie fera l'objet du paragraphe suivant.
Interprétation
Donner une interprétation économique du
vecteur
. A partir de la solution réalisable
, on construit le point
obtenu en augmentant d'une unité la
-ième variable
hors base. D'après l'égalité
BNyN
, ce point vaut
, où
désigne le
-ième vecteur de la base canonique de
. Si
le point ainsi obtenu est réalisable, on obtient :
Pour un problème de type maximisation, cette dernière
égalité s'écrit
. Donc, l'élément
représente la quantité s'ajoutant à
la valeur économique
lorsqu'on incrémente d'une unité
la
coordonnée hors base de
, pour autant que le
nouveau point obtenu soit réalisable. Semblablement, lorsqu'il s'agit d'un
problème de minimisation,
correspond à la valeur retranchée de la
valeur économique. C'est la raison pour
laquelle
s'appelle vecteur des coûts réduits (ou
coûts fictifs ou encore coûts marginaux).
Exercice
Sommet-Base-Optimalité : A venir
Optimisation linéaire
→
IV Méthode du simplexe
→
IV-5 Algorithme du simplexe
→ IV-5-1 Condition d'optimalité
IV-5-2 Amélioration de la fonction d'objectif
Optimisation linéaire
→
IV Méthode du simplexe
→
IV-5 Algorithme du simplexe
→ IV-5-2 Amélioration de la fonction d'objectif
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
On se donne une base réalisable . Le vecteur désigne la colonne de qui est à fortiori une colonne de . On note aussi la colonne d'indice de la matrice . D'ailleurs, n'est autre où est le -ième vecteur de la base canonique de .
Théorème
On suppose que la base réalisable
vérifie
. Il existe donc une composante
du
vecteur
qui est strictement positive. Considérons le
vecteur colonne
de la matrice
. Alors de deux choses l'une
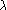 est
atteint (i.e.
). Alors,
la matrice
, obtenue à partir de
en remplaçant le vecteur colonne
par
, est une base réalisable. La solution de base
associée à
vérifie
De plus, on a
, selon que
(FS) soit de tupe maximisation ou minilisation. Ici, le point
représente la solution de base réalisable associée
à
:
.
est
atteint (i.e.
). Alors,
la matrice
, obtenue à partir de
en remplaçant le vecteur colonne
par
, est une base réalisable. La solution de base
associée à
vérifie
De plus, on a
, selon que
(FS) soit de tupe maximisation ou minilisation. Ici, le point
représente la solution de base réalisable associée
à
:
.
- (i) ou bien , et dans ce cas l'optimum est infini,
- (ii) ou bien
. Dans ce cas, on
calcule le réel
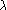 est
atteint (i.e.
). Alors,
la matrice
, obtenue à partir de
en remplaçant le vecteur colonne
par
, est une base réalisable. La solution de base
associée à
vérifie
est
atteint (i.e.
). Alors,
la matrice
, obtenue à partir de
en remplaçant le vecteur colonne
par
, est une base réalisable. La solution de base
associée à
vérifie
Il est intéressant de remarquer que dans le cas où la base réalisable est non dégénérée, le paramètre
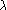 est strictement positif. Sans aucun doute, le point
construit
possède, en cas de non dégénérescence,
une valeur économique strictement meilleure que celle de
.
est strictement positif. Sans aucun doute, le point
construit
possède, en cas de non dégénérescence,
une valeur économique strictement meilleure que celle de
.
Optimisation linéaire
→
IV Méthode du simplexe
→
IV-5 Algorithme du simplexe
→ IV-5-2 Amélioration de la fonction d'objectif
IV-5-3 Algorithme
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
/* On suppose que l'on dispose d'une base réalisable */
tant que faire
choisir telle que
si alors
optimum infini /* */
exit
sinon
calculer
déterminer pour lequel
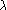 est atteint
est atteint/* est remplacée par */
/* est remplacée par */
Calculer
Optimum atteint en et il vaut
/* Fin de l'algorithme */
IV-5-4 Règle de pivotage
Optimisation linéaire
→
IV Méthode du simplexe
→
IV-5 Algorithme du simplexe
→ IV-5-4 Règle de pivotage
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Dans la pratique, le choix de est souvent multiple, il se peut que plusieurs composantes soient strictement positives. Etant donnée que la nouvelle solution vérifie :
Il arrive aussi que le minimum
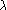 soit atteint pour deux ou plusieurs
coordonnées différentes. Dans ce cas de figure, on fixe
comme critère de choix pour l'indice
, la première
coordonnée trouvée
qui réalise le minimum
soit atteint pour deux ou plusieurs
coordonnées différentes. Dans ce cas de figure, on fixe
comme critère de choix pour l'indice
, la première
coordonnée trouvée
qui réalise le minimum
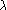 .
Pour des raisons de stabilité numérique et par analogie avec
la méthode de Gauss avec pivot partiel,
un autre critère de choix est souvent considéré. Il consiste
à choisir
de façon à ce que
soit le plus élevé parmi les éléments
strictement positifs.
Le critère qui fixe le choix de
et de l'indice
s'appelle règle de pivotage. La règle qui prend systématique la plus grande valeur positive de
s'appelle
règle du meilleur coût marginal, c'est cette règle que l'on
adopte dans ce cours.
.
Pour des raisons de stabilité numérique et par analogie avec
la méthode de Gauss avec pivot partiel,
un autre critère de choix est souvent considéré. Il consiste
à choisir
de façon à ce que
soit le plus élevé parmi les éléments
strictement positifs.
Le critère qui fixe le choix de
et de l'indice
s'appelle règle de pivotage. La règle qui prend systématique la plus grande valeur positive de
s'appelle
règle du meilleur coût marginal, c'est cette règle que l'on
adopte dans ce cours.
Optimisation linéaire
→
IV Méthode du simplexe
→
IV-5 Algorithme du simplexe
→ IV-5-4 Règle de pivotage
V Algorithme du simplexe standard
Optimisation linéaire
→ V Algorithme du simplexe standard
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Dans ce chapitre, les données mise en oeuvre dans l'algorithme du simplexe seront représentées dans un tableau. A chaque itération correspond un tableau appelé tableau simplexe. Des formules itératives liant les éléments d'un tableau au tableau subséquent seront également établies.
Optimisation linéaire
→ V Algorithme du simplexe standard
V-1 Tableau simplexe
Optimisation linéaire
→
V Algorithme du simplexe standard
→ V-1 Tableau simplexe
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Les éléments qui interviennent dans l'algorithme du simplexe peuvent être récapitulés dans ce qui suit.
- Les variables de base et les variables hors base. La base réalisable et la matrice seront immédiatement identifiées à partir des variables de base et hors base.
- La solution associée à la base réalisable . Puisque , on ne retient que le vecteur .
- Le vecteur pour tester l'optimalité.
- La matrice
afin de calculer
et le
coefficient
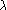 .
.
- La valeur de la fonction
au point
qui est égale à
 | ||
Les coordonnées correspondent aux variables de base, et les coordonnées correspondent aux variables hors base. Le terme désigne la valeur de la fonction d'objectif au point réalisable . D'après l'indexation des variables de base, on a :
Optimisation linéaire
→
V Algorithme du simplexe standard
→ V-1 Tableau simplexe
V-2 Application
Optimisation linéaire
→
V Algorithme du simplexe standard
→ V-2 Application
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Comme application de l'algorithme du simplexe, nous allons résoudre les trois exemples du premier chapitre en utilisant les tableaux simplexe.
Optimisation linéaire
→
V Algorithme du simplexe standard
→ V-2 Application
V-2-1 Exemple 1
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Reprenons l'Exemple 1 :
-
On écrit ce probème sous forme standard.
En ajoutant les variables d'écart, on obtient :
-
On cherche un système de variables de base réalisable
Il est clair que forme un système de variables de base réalisable. La base associée est , elle vérifie bienPour cette base, on obtient :car etRappelons que les coordonnées de chaque solution de base réalisable sont classées selon et . Pour la base , si on écrit les coordonnées de la solution réalisable dans l'ordre , , on obtient exactement le point .
-
Itération 1
1
5
Le vecteur ligne n'est pas négatif, il contient deux composantes strictement positives. Il a été convenu de choisir la plus grande qui est 5. Pour distinguer notre choix, on décide de l'écrire en gras. Faisant référence aux notations utilisées dans le Théorème , on a :Donc, au cours de l'itération suivante, la variable hors base qui se situe au niveau de va devenir une variable de base. D'après le tableau ci-dessus, il s'agit de la variable . Pour déterminer la variable qui prend place, il va falloir calculer le paramètre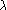 et en déduire l'indice
.
D'après le même tableau, on a :
et donc L'indice correspond alors à la variable . On décide de mettre en gras l'élément qui a permis de réaliser le minimumEn résumé, lorsqu'on écrit en gras une composante de , cela signifie que la variable, figurant sur la même colonne que du tableau simplexe, entre dans la base. Inversement, l'identification de permet de décider que la variable, située sur la même ligne que sort de la base. Naturellement, ces deux variables s'appellent respectivement variable entrante et variable sortante.
et en déduire l'indice
.
D'après le même tableau, on a :
et donc L'indice correspond alors à la variable . On décide de mettre en gras l'élément qui a permis de réaliser le minimumEn résumé, lorsqu'on écrit en gras une composante de , cela signifie que la variable, figurant sur la même colonne que du tableau simplexe, entre dans la base. Inversement, l'identification de permet de décider que la variable, située sur la même ligne que sort de la base. Naturellement, ces deux variables s'appellent respectivement variable entrante et variable sortante.
-
Itération 2
A ce stade de calcul, la base réalisable est associée aux variables . Pour la prochaine itération, on aura besoin de à la place de . Afin de ne pas encombrer le texte par les notations, il est naturel de garder les mêmes symboles , et
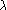 pour toutes les itérations du
simplexe. En tenant compte de l'ordre des indices
des variables de base et de
, on obtient
Par un simple calcul, on vérifie les égalités suivantes :Le tableau simplexe relatif à cette itération est
pour toutes les itérations du
simplexe. En tenant compte de l'ordre des indices
des variables de base et de
, on obtient
Par un simple calcul, on vérifie les égalités suivantes :Le tableau simplexe relatif à cette itération est
1 4
Noter que le vecteur peut être calculé aussi via la formule

= =
De même, la valeur qui correspond à peut être obtenue à travers le résultat Ces deux constatations restent valables pour les itérations qui suivent et pour n'importe quel exemple.
Pour ce tableau, le vecteur admet une seule composante strictement positive qui est . Donc, la variable entre dans la base au cours de l'itération 3. En ce qui concerne le nouveau paramètre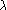 , on a :
Ainsi, la variable devient hors base. Il est intéressant de noter que les matrices et peuvent être déduites du tableau simplexe à partir des variables de base et des variables hors base. Dans toute la suite et lors de l'exécution d'une itération simplexe, seul le tableau simplexe sera donné. Bien entendu, on précisera en gras les éléments et et on calculera le coefficient
, on a :
Ainsi, la variable devient hors base. Il est intéressant de noter que les matrices et peuvent être déduites du tableau simplexe à partir des variables de base et des variables hors base. Dans toute la suite et lors de l'exécution d'une itération simplexe, seul le tableau simplexe sera donné. Bien entendu, on précisera en gras les éléments et et on calculera le coefficient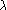 , à chaque fois que cela
s'avère nécessaire.
, à chaque fois que cela
s'avère nécessaire.
-
Itération 3
3 3 -
Itération 4
- Conclusion
V-2-2 Exemple 2
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Pour l'Exemple 2, le (PL) considéré est
-
On écrit ce probème sous forme standard.
En retranchant une variable d'écart à la première contrainte, et en ajoutant une seconde à la deuxième, on obtient :
-
On cherche un système de variables de base réalisable
Prenons par exemple et montrons qu'il forme un système de variables de base réalisable. La matrice associée à ce système vérifie :Les composantes de étant positives, la matrice est une base réalisable. On calculeetLa solution de base réalisable relative à est , elle donne une valeur d'objectif égale à .
-
Itération 1
412 -
Itération 2
Le vecteur ligne étant négatif, la solution associée est optimale pour (FS). Compte tenu du Théorème , on peut affirmer que est une solution optimale de ce (PL) et que la valeur maximale de sur le domaine réalisable est .
-
Remarque
On avait montré à l'aide du graphique que ce probème admettait une infinité de solutions optimales. Ce résultat peut être retrouvé via le dernier tableau simplexe. En effet, on remarque sur ce tableau une composante nulle. Le vecteur est égal à , qui est négatif. Donc, tout point de la forme est réalisable pour (FS) et ceci pour tout réel
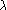 positif. Du fait que
, la valeur de
, qui est égale à
, reste inchangée. Par suite, le point
est optimal pour (FS) quelque soit le réel
positif
positif. Du fait que
, la valeur de
, qui est égale à
, reste inchangée. Par suite, le point
est optimal pour (FS) quelque soit le réel
positif
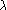 .
.
-
Conclusion
En ce qui concerne le (PL) associé, nous allons utiliser comme d'habitude le Théorème . Si on classe les composantes de dans l'ordre , , on obtient . Par conséquent,est un point optimal pour (PL). Notons que est un vecteur directeur de la droite (voir Figure ). D'ailleurs, la demi-droite co''{3}ncide avec l'ensemble des points lorsque
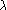 décrit
.
décrit
.
V-2-3 Exemple 3
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Pour l'Exemple 3 :
-
On écrit ce problème sous forme standard
On a :
-
On cherche un système de variables de base réalisable
Il est facile de vérifier que est une base réalisable.
-
Itération 1
1
-
Conclusion
Pour écrit en gras, on a . Donc, d'après le Théorème , le probème vérifie :Plus précisément, pour tout réel , le point réalisable possède une valeur d'objectif égale à :dont la limite en vaut . Le point est égal àet par conséquent est un point réalisable du (PL) initial et ceci pour tout réel . Noter que décrit le demi axe lorsque
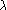 parcourt l'ensemble des réels positifs. D'après la
Figure
, tous ces points sont effectivement réalisables.
parcourt l'ensemble des réels positifs. D'après la
Figure
, tous ces points sont effectivement réalisables.
V-3 Sommets et solutions de base
Optimisation linéaire
→
V Algorithme du simplexe standard
→ V-3 Sommets et solutions de base
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Tous les (PL) résolus jusqu'ici sont des formes canoniques puisque le domaine réalisable de chacun peut s'écrire sous la forme
Optimisation linéaire
→
V Algorithme du simplexe standard
→ V-3 Sommets et solutions de base
V-4 Formules itératives
Optimisation linéaire
→
V Algorithme du simplexe standard
→ V-4 Formules itératives
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
A chaque itération de l'algorithme du simplexe, on est contraint à calculer la matrice et le vecteur ligne . Ces calculs exigent préalablement la détermination de la matrice inverse . Dans cette section, nous allons voir comment surmonter cette difficulté. Tout simplement, on évitera le calcul de . Les éléments d'un tableau vont être déterminés itérativement à partir des éléments du tableau précédent.
Optimisation linéaire
→
V Algorithme du simplexe standard
→ V-4 Formules itératives
V-4-1 Matrice du pivot
Optimisation linéaire
→
V Algorithme du simplexe standard
→
V-4 Formules itératives
→ V-4-1 Matrice du pivot
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Posons la matrice réelle rectangulaire avec . Aussi, on pose et où (resp. ) désigne la colonne de (resp. ). Supposons qu'à l'itération relative à la base , on ait permuté le vecteur colonne avec . Au niveau du tableau, cela revient à écrire en gras l'élément de la matrice
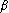 , que l'on
note communément
. Par conséquent, au cours de la
prochaine itération, on aura
, que l'on
note communément
. Par conséquent, au cours de la
prochaine itération, on aura
Théorème
Afin de mieux visualiser les formules établies dans le Théorème , nous allons illustrer tout d'abord les éléments du tableau simplexe dans le schéma suivant. Le réel { } correspond à l'élément écrit en gras au niveau de la matrice .
Ensuite, le tableau simplexe qui suit sera rempli moyennant des transformations qui peuvent être résumées en ces termes :
- au niveau de { }, on aura .
- Tout élément de la colonne relative à { } devient .
- Tout élément de la ligne relative à { } devient .
- Tout élément en dehors de la ligne et de la colonne relative à { } sera transformé en . Dans cette dernière expression, on tient à préciser que ( resp. ) est l'élément de la matrice qui appartient à la même colonne (resp. ligne) que et la même ligne (resp. colonne) que { }.
Optimisation linéaire
→
V Algorithme du simplexe standard
→
V-4 Formules itératives
→ V-4-1 Matrice du pivot
V-4-2 Vecteur des coûts réduits
Optimisation linéaire
→
V Algorithme du simplexe standard
→
V-4 Formules itératives
→ V-4-2 Vecteur des coûts réduits
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
On garde ici le même pivot . Cela veut dire que le vecteur colonne a été échangé par et vice versa. Les formules établies précédemment pour vont conduire aux relations liant les composantes de avec celles de . Pour cela, on pose :
Théorème
D'ores et déjà, on peut observer que les relation liant à sont les mêmes que les relations entre une ligne et une ligne en dehors de la ligne du pivot . Le terme , qu'on a convenu d'écrire en gras, se situe sur la même colonne du pivot. Il est remplacé par . Les opérations qu'il faut appliquer sur , , en vue d'obtenir sont identiques à celles effectuées sur les termes de symbole dans le schéma du paragraphe précédent.
Optimisation linéaire
→
V Algorithme du simplexe standard
→
V-4 Formules itératives
→ V-4-2 Vecteur des coûts réduits
V-5 Algorithme du simplexe standard
Optimisation linéaire
→
V Algorithme du simplexe standard
→ V-5 Algorithme du simplexe standard
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
En ce qui concerne le vecteur , il a été indiqué d'avance qu'il peut être déterminé par les relations
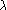 par sa valeur
, on obtient les mêmes formules qui
régissent une colonne de
par sa valeur
, on obtient les mêmes formules qui
régissent une colonne de
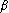 en dehors de la colonne du
pivot. Maintenant, l'élément en bas à droite du tableau simplexe, à
savoir
, se calcule itérativement via la relation
ou
selon que le probème
étudié soit de type maximisation ou minimisation. En tenant
compte de l'expression de
en dehors de la colonne du
pivot. Maintenant, l'élément en bas à droite du tableau simplexe, à
savoir
, se calcule itérativement via la relation
ou
selon que le probème
étudié soit de type maximisation ou minimisation. En tenant
compte de l'expression de
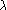 , il est facile de constater que
la formule
s'identifie à la formule
relative à un élément de symbole ''
''. Afin de garder les
mêmes formules, il est souhaitable de remplacer
par
lorsqu'il s'agit d'un probème de type maximisation. Au niveau de
l'implémentation sur machine, il est commode de définir une
matrice, que l'on note
, qui contient les éléments
, il est facile de constater que
la formule
s'identifie à la formule
relative à un élément de symbole ''
''. Afin de garder les
mêmes formules, il est souhaitable de remplacer
par
lorsqu'il s'agit d'un probème de type maximisation. Au niveau de
l'implémentation sur machine, il est commode de définir une
matrice, que l'on note
, qui contient les éléments
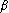 ,
,
et
:
,
,
et
:
Algorithme du simplexe standard
Input: base réalisable
Initialiser , et
Calculer
tant que faire
déterminer l'indice pour lequel le maximum est atteint
si alors
optimum infini /* ou */
exit
sinon
calculer
déterminer l'indice pour lequel
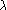 est atteint
est atteintCalculer
Optimum vaut
Une solution optimale, que l'on note , est donnée par :
Exercice
Résolution par les tableaux simplexe
Méthode du simplexe
Méthode du simplexe
Optimisation linéaire
→
V Algorithme du simplexe standard
→ V-5 Algorithme du simplexe standard
VI Dualité en programmation linéaire
Optimisation linéaire
→ VI Dualité en programmation linéaire
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Dans le cadre de la programmation linéaire, on peut associer à chaque (PL) un autre (PL), de type opposé, nommé programme dual. Leurs propriétés sont étroitement liées :
Par souci d'optimiser les calculs lors de la résolution d'un (PL), il est plus avantageux, dans certaines circonstances, de résoudre le probème dual. Ensuite, la solution du (PL) initial sera déduite facilement par l'intermédiaire de la solution du dual.
Une des conséquences les plus fructueuses de la notion de dualité est l'algorithme dual-simplexe qui a été conçu, dans les années , par Lemke. Cet algorithme a un intérêt inéluctable en programmation linéaire.
Optimisation linéaire
→ VI Dualité en programmation linéaire
VI-1 Primal - Dual
Optimisation linéaire
→
VI Dualité en programmation linéaire
→ VI-1 Primal - Dual
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Optimisation linéaire
→
VI Dualité en programmation linéaire
→ VI-1 Primal - Dual
VI-1-1 Cas d'une forme canonique
Optimisation linéaire
→
VI Dualité en programmation linéaire
→
VI-1 Primal - Dual
→ VI-1-1 Cas d'une forme canonique
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
On considère un programme linéaire écrit sous forme canonique que l'on suppose de type maximisation :
Optimisation linéaire
→
VI Dualité en programmation linéaire
→
VI-1 Primal - Dual
→ VI-1-1 Cas d'une forme canonique
VI-1-2 Cas général
Optimisation linéaire
→
VI Dualité en programmation linéaire
→
VI-1 Primal - Dual
→ VI-1-2 Cas général
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Tout programme linéaire ne s'écrit pas forcément sous forme canonique. Il peut admettre en effet des contraintes d'égalités et/ou des variables sans restriction de signe (s.r.s. en abrégé). De ce fait, la forme générale d'un primal de type maximisation s'écrit de la façon suivante :
Optimisation linéaire
→
VI Dualité en programmation linéaire
→
VI-1 Primal - Dual
→ VI-1-2 Cas général
VI-1-3 Tableau récapitulatif
Optimisation linéaire
→
VI Dualité en programmation linéaire
→
VI-1 Primal - Dual
→ VI-1-3 Tableau récapitulatif
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
On note que lorsque le primal est écrit sous une forme générale, son dual l'est aussi. Le tableau ci-dessous récapitule les règles de correspondance entre un primal de type maximisation et son dual.
Primal | Dual |
| - Maximisation | - Minimisation |
| - Coefficients d'objectif | - Second membre |
| - Second membre | - Coefficients d'objectif |
| - Matrice régissant les contraintes | - Matrice transposée |
- Relation liant les contraintes
| - Nature des variables
|
- Nature des variables
| - Relation liant les contraintes
|
Remarque
On aurait pu choisir comme primal un
probème de minimisation, le dual aurait été alors un
programme linéaire de type maximisation. Tout simplement parce que le dual du dual
est le primal (facile à prouver).
Autrement dit, si on permutait dans le tableau
précédent les deux mots Primal et Dual, on obtiendrait les règles
de correspondance entre un primal de minimisation et son dual.
Optimisation linéaire
→
VI Dualité en programmation linéaire
→
VI-1 Primal - Dual
→ VI-1-3 Tableau récapitulatif
VI-2 Optimalité pour le primal-dual
Optimisation linéaire
→
VI Dualité en programmation linéaire
→ VI-2 Optimalité pour le primal-dual
- I Programmation linéaire
- II Méthode graphique
- III Méthode des sommets
- IV Méthode du simplexe
- V Algorithme du simplexe standard
- VI Dualité en programmation linéaire
- Index
Théorème
Si
et
sont deux solutions réalisables de
et
respectivement, alors
.
Si de plus on a
, alors
et
sont
deux solutions optimales de
et
respectivement.
Dans la pratique, il est souvent difficile de trouver deux points réalisables et de et tels que . La situation la plus envisageable consiste à déterminer une solution optimale du primal via par exemple le simplexe, puis essayer d'en dégager une solution optimale du dual.
Théorème
Soit
une base réalisable de la forme standard
relative au primal
. Si la base
vérifie
, alors
est une solution optimale du dual
.
Remarque
Afin de déterminer la solution optimale
,
il est inutile de calculer la matrice inverse
. Il suffit, en effet, de résoudre le système de
Cramer
. Par ailleurs, le Théorème
précédent n'exige aucune condition sur la nature du primal (
ou
).
Optimisation linéaire
→
VI Dualité en programmation linéaire
→ VI-2 Optimalité pour le primal-dual