OEF Courbes paramétrées
--- Introduction ---
Ce module regroupe pour l'instant 9 exercices sur les courbes paramétrées.
Longueur d'arc paramétrée 2D
Calculer la longueur de la courbe paramétrée
,
entre
et
.
xrange , yrange , trange , arrow ,0,,0,10,grey arrow 0,,0,,10,grey plot skyblue,, trange , linewidth 3 plot blue,,
Veuillez donner votre réponse avec une précision d'au moins 4 chiffres après la virgule.
Point double cubique
Nous avons une courbe paramétrée ci-dessous, définie par
,
pour
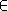 [,]. Déterminez le point double de la courbe.
[,]. Déterminez le point double de la courbe.
r=2.5 xrange -r,r yrange -r,r trange -2,2 fill 0,0,white arrow -r,0,r,0,10,grey arrow 0,-r,0,r,10,grey text grey,0.88*r,0.16*r,small,x text grey,0.07*r,0.95*r,small,y disk ,,8,red plot blue,,
Réponse : le point double est (
=
,
=
)
correspondant aux deux valeurs de
=
et
=
. Précision exigée : au moins 4 chiffres après la virgule.
Tangentes plates cubiques
Nous avons une courbe paramétrée ci-dessous, définie par
,
pour
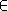 [,].
[,].
Donnez une valeur de
pour laquelle la tangente de la courbe est :
Dans ce cas, cette tangente a pour équation
=
.
(Précision exigée : au moins 4 chiffres après la virgule.)
Tangentes obliques cubiques
La courbe paramétrée ci-dessous, est définie par
,
pour
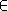 [,].
[,].
Donnez une valeur de
pour laquelle la tangente de la courbe est de la forme
:
=
. Dans ce cas, on a
=
. (Précision exigée : au moins 4 chiffres après la virgule.)
Longueur point double
Nous avons une courbe paramétrée ci-dessous, définie par
,
pour
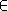 [,]. Déterminez le point double de la courbe, ainsi que la longueur de la partie entre les deux passages au point double.
[,]. Déterminez le point double de la courbe, ainsi que la longueur de la partie entre les deux passages au point double.
r=2.5 xrange -r,r yrange -r,r trange -2,2 fill 0,0,white arrow -r,0,r,0,10,grey arrow 0,-r,0,r,10,grey text grey,0.88*r,0.16*r,small,x text grey,0.07*r,0.95*r,small,y disk ,,8,red plot skyblue,, trange , linewidth 2 plot blue,,
Réponse : le point double est (
=
,
=
)
correspondant aux deux valeurs de
=
et
=
.
La longueur de la partie de courbe est
.
(Précision exigée : au moins 4 chiffres après la virgule.)
Points stationnaires
Soit la courbe paramétrée
d'équations paramétriques
pour
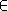 [-1,1]. On écrit pour
sur
,
[-1,1]. On écrit pour
sur
,
Calculer le plus petit indice
pour lequel
est non nul. Que vaut
?
Calculer le plus petit indice
tel que les vecteurs
et
forment un système libre de
. Que vaut
?
Voici les vecteurs
et
que vous avez trouvé. Ils déterminent 4 quadrans I, II, III, IV .
xrange -(), yrange -(), segment ,,black segment ,, black fill , blue fill ,yellow fill ,grey fill ,orange dhline ,,black arrow (),(),()+1,(), 5, black arrow (),(),(),()+1, 5, black dvline ,,black linewidth 2 arrow 0,0,, 10, navy arrow 0,0,, 10,navy text black , , medium, vp text black , , medium, vq text black,,large, I text black, ,large, II text black, ,large, III text black, ,large, IV
Dans quel cadran se trouve la courbe lorsque
est et proche de 0 :
? Dans quel cadran se trouve la courbe lorsque
est et proche de 0 :
?
Le point de paramètre 0 est un
Tangente et points stationnaires
Soit la courbe paramétrée
d'équations paramétriques
pour
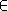 [-1,1]. Calculer un vecteur tangent à la courbe au point
et donner l'équation de la tangente en ce point.
[-1,1]. Calculer un vecteur tangent à la courbe au point
et donner l'équation de la tangente en ce point.
Tableau de variation alpha
Nous avons une courbe paramétrée
, donnée par
, pour
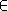 [,]. Voici les tableaux de variation des deux fonctions. Parmi les courbes suivantes, laquelle correspond à
?
[,]. Voici les tableaux de variation des deux fonctions. Parmi les courbes suivantes, laquelle correspond à
?
plot blue, A
plot blue, B
plot blue, C
plot blue, D
Tableau de variation alpha II
Nous avons une courbe paramétrée
, donnée par
, pour
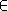 [,]. Voici les tableaux de variation des deux fonctions.
Parmi les courbes suivantes, laquelle correspond à
?
[,]. Voici les tableaux de variation des deux fonctions.
Parmi les courbes suivantes, laquelle correspond à
?
plot blue, A
plot blue, B
plot blue, C
plot blue, D
Dans ce dessin de la courbe
plot blue, disk ,,6,red
, le point rouge correspond à une valeur
. A quel intervalle appartient
? A. [,] B. [,] C. [,] D. [,]
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: collection d'exercices sur les courbes paramétrées. Plateforme WIMS d'exercices interactifs et gratuits à données aléatoires avec feedback et corrections automatiques de l'enseignement secondaire au supérieur hébergée par le rectorat de l'académie de Versailles
- Keywords: euler, wims, eulerwims, versailles, mathématiques, mathematics, math, maths, physique, sciences, exercices, exercices à données aléatoires avec correction automatique, exercise, interactif, interactive mathematics, interactive math, interactive maths, en ligne, online, calcul, calculus, géométrie, geometry, courbes, curve, graphing, statistiques, statistics, probabilités, probability, algorithmes, algèbre, analyse, arithmétique, fonctions, qcm, quiz, cours, devoirs, éducation, enseignement, teaching, gratuit, free, open source, communs numériques, plateforme, classe virtuelle, virtual class, virtual classes, virtual classroom, virtual classrooms, interactive documents, interactive document, exercices interactifs, correction, feedback, lexique, glossaire, examen, feuilles d'exercices, ressources, outils, création d'exercices, codage, activités, parcours d'apprentissage, mathematics, analytic_geometry,, parametric_curves, function_variation, polar_curves
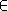 [,]. Déterminez le point double de la courbe.
[,]. Déterminez le point double de la courbe. 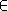 [,].
[,]. 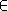 [,].
[,]. 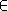 [,]. Déterminez le point double de la courbe, ainsi que la longueur de la partie entre les deux passages au point double.
[,]. Déterminez le point double de la courbe, ainsi que la longueur de la partie entre les deux passages au point double. 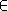 [-1,1]. On écrit pour
sur
,
[-1,1]. On écrit pour
sur
, 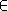 [-1,1]. Calculer un vecteur tangent à la courbe au point
et donner l'équation de la tangente en ce point.
[-1,1]. Calculer un vecteur tangent à la courbe au point
et donner l'équation de la tangente en ce point.
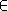 [,]. Voici les tableaux de variation des deux fonctions.
[,]. Voici les tableaux de variation des deux fonctions. 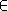 [,]. Voici les tableaux de variation des deux fonctions.
[,]. Voici les tableaux de variation des deux fonctions.