Arithmétique modulaire
Guide
La première partie de ce document est une introduction de l'anneau à partir des congruences.La deuxième partie met l'accent sur quelques résolutions de problèmes où l'utilisation des congruences est fondamentale ou simplement pratique. Ce document n'a aucune prétention à être complet ni même achevé. On espère qu'il peut être utile ainsi.
Définition et opérations algébriques
Définition
Définition
Une classe de congruence modulo
est un sous-ensemble de
de la forme
avec
un entier.
L'ensemble des classes de congruences modulo
est noté
. On note aussi
.
Un entier
est appelé un représentant de la
classe
si
et
sont congrus modulo
.
Exemple
- Les classes et sont égales.
- Les classes et sont différentes.
- L'entier est un représentant de la classe .
Le reste de la division euclidienne de
par
est
bien un représentant de
mod
qui est compris entre 0 et
.
Mais il est quelquefois commode de prendre les représentants entre et et même de les prendre quelconques.
Exercice
Classes
Exemple pour plus tard
Il est quand même
plus facile de calculer la puissance
-ième de la classe
en utilisant
le représentant de cette classe qu'est -1. Ainsi :
.
Opérations
Définition.
On définit les opérations algébriques d'addition,
soustraction, multiplication par
Mais nous écrirons souvent mod , par exemple
,
et même
,
.
On peut voir ici quelques tables d'
addition
ou de
multiplication.
Théorème.
est un anneau commutatif.
Exercices
- Opérations ,
- Carrés
- Somme et produit
Table d'addition
Voici la table d'addition dans :| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 0 |
| 2 | 2 | 3 | 4 | 5 | 6 | 0 | 1 |
| 3 | 3 | 4 | 5 | 6 | 0 | 1 | 2 |
| 4 | 4 | 5 | 6 | 0 | 1 | 2 | 3 |
| 5 | 5 | 6 | 0 | 1 | 2 | 3 | 4 |
| 6 | 6 | 0 | 1 | 2 | 3 | 4 | 5 |
Table de multiplication
Voici la table de multiplication dans : | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 0 | 2 | 4 | 6 | 8 | 0 | 2 | 4 | 6 | 8 |
| 3 | 0 | 3 | 6 | 9 | 2 | 5 | 8 | 1 | 4 | 7 |
| 4 | 0 | 4 | 8 | 2 | 6 | 0 | 4 | 8 | 2 | 6 |
| 5 | 0 | 5 | 0 | 5 | 0 | 5 | 0 | 5 | 0 | 5 |
| 6 | 0 | 6 | 2 | 8 | 4 | 0 | 6 | 2 | 8 | 4 |
| 7 | 0 | 7 | 4 | 1 | 8 | 5 | 2 | 9 | 6 | 3 |
| 8 | 0 | 8 | 6 | 4 | 2 | 0 | 8 | 6 | 4 | 2 |
| 9 | 0 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Inverses et diviseurs de zéro
Existence d'un inverse pour la multiplication
Théorème.
Soit un entier
premier à
.
Alors
est inversible dans
, c'est-à-dire qu'il existe
tel que
.
En fait, il s'agit d'une
équivalence :
La démonstration donne aussi un moyen de
calcul de cet inverse.
Théorème.
Soit un entier
. Alors
est inversible dans
si et seulement si
est premier à
.
L'entier
est premier avec
si et seulement s'il existe
et
dans 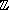 tels que
tels que
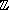 tels que
tels que Donc,
- si est premier avec , il existe un entier tel que et est inversible dans .
- Si est inversible dans , il existe un entier tel que . Par définition de la congruence, cela signifie qu'il existe un entier tel que et on a , donc et sont premiers entre eux.
Exemple
Prenons
:
| a = 0 |
0   1 5 1 5
|
| a = 1 |
1   1 5 1 5
|
| a = 2 |
2   1 5 1 5
|
| a = 3 |
3   1 5 1 5
|
| a = 4 |
4   1 5 1 5
|
Exercices
- Inverse : 1 2 3
- Division : I II III
Exemples
Exemple
Prenons
:
Lorsque
n'a pas d'inverse, on voit qu'il est alors diviseur de zéro,
c'est-à-dire que
| a=0 | |
| a=1 | |
| a=2 | |
| a=3 | |
| a=4 | |
| a=5 |
pour un entier
.
Exemple
Pour
| a=0 | a=18 | ||
| a=1 | a=19 | ||
| a=2 | a=20 | ||
| a=3 | a=21 | ||
| a=4 | a=22 | ||
| a=5 | a=23 | ||
| a=6 | a=24 | ||
| a=7 | a=25 | ||
| a=8 | a=26 | ||
| a=9 | a=27 | ||
| a=10 | a=28 | ||
| a=11 | a=29 | ||
| a=12 | a=30 | ||
| a=13 | a=31 | ||
| a=14 | a=32 | ||
| a=15 | a=33 | ||
| a=16 | a=34 | ||
| a=17 |
Cas où n est premier
Théorème.
Si
est un nombre premier, tout nombre non nul dans
a un inverse.
Démonstration.
Comme
est premier, il est premier avec tout nombre qu'il ne divise pas,
c'est-à-dire avec tout nombre dont la classe de congruence modulo
n'est pas nul.
On applique alors le
théorème:
Théorème.
Soit un entier
. Alors
est inversible dans
si et seulement si
est premier à
.
Exercices
- Puissance
- Calcul de puissances : I II
Diviseurs de 0
Lorsque n'a pas d'inverse, on voit qu'il est alors diviseur de zéro, c'est-à-dire quepour un entier .
Proposition.
Dans
,
est un diviseur de zéro si et seulement si
n'est pas premier avec
.
Démonstration.
-
Si
est diviseur de zéro, il n'est pas inversible donc d'après le
théorème
Théorème.
Soit un entier . Alors est inversible dans si et seulement si est premier à ., il n'est pas premier avec . -
Si
n'est pas premier avec
, soit
le pgcd de
et de
.
Soit
le quotient de
par
; on a
, et .
Donc mod . La classe de modulo est non nulle, car est un diviseur strict de .
Exemple
Pour
Exercices
Diviseurs de zéro
1
2
3
Résolution de quelques problèmes
- Résolution de l'équation linéaire
- Équation diophantienne linéaire à 3 inconnues
- Petit théorème de Fermat
- Résolution d'équations du type
- Pour aller plus loin
Résolution de l'équation linéaire
La question est de trouver tous les entiers vérifiant l'équation.
On peut adopter plusieurs points de vue selon qu'on est à l'aise ou non dans l'anneau .Première étape :
L'équation
a une solution
si et seulement si le pgcd
de
et de
divise
.
Dans ce cas, on divise l'équation par
(y compris
)
et on est ramené au cas où
et
sont premiers entre eux.
Deuxième étape :
-
Première méthode : travailler dans
il s'agit de trouver les entiers tels qu'il existe un entier vérifiantou encoreOn s'est donc ramené à résoudre une équation de Bezout. Elle a une solution car on a supposé que et sont premiers entre eux.
-
Deuxième méthode : travailler dans
Comme et sont premiers entre eux, il existe et tel que . En particulier, il existe un entier tel que . On multiplie l'équation par , ce qui donneEn fait il s'agit de la démonstration de ce que est inversible dans et que si , est l'inverse de dans .et donc commeet on a résolu le problème.
Exercice rapide
Équation linéaire modulaire
Exercice
Équation linéaire
Petit théorème de Fermat
Théorème.
Soit
un nombre premier impair. Alors pour tout entier
,
On en déduit le
théorème de Fermat :
.
Théorème.
Soit
un nombre premier impair. Alors pour tout entier
premier à
,
.
Théorème.
Soit
un nombre premier impair. Soit
un entier premier à
. Alors,
- il existe un plus petit entier tel que , cet entier est un diviseur de ;
- les entiers vérifiant sont exactement les multiples de .
Par le petit théorème de Fermat, l'ensemble des entiers
strictement positifs vérifiant
est non vide
car il contient
. Il admet donc un plus petit élément. Notons-le
.
Faisons la division euclidienne de
par
:
avec
entier positif
. On a
d'où
Donc, par minimalité de
,
est soit plus grand que
, soit nul.
Donc
est nul, et
divise
.
Résolution d'équations du type
Il faut quand même préciser qui est l'inconnue ! Cela peut être ou .On prend un nombre premier.
-
Les équations du type
peuvent être traitées en utilisant
le
Théorème de Fermat
Théorème.
Soit un nombre premier impair. Alors pour tout entier premier à ,et ses conséquences : Les solutions de cette équation sont les multiples d'un diviseur de à trouver. On prend donc tous les diviseurs de et on les essaye ! (on peut quand même réfléchir au moyen de ne pas faire trop de calculs : si n'est pas congru à 1 modulo , pas la peine d'essayer ou ).. -
Les équations du type
avec
premier
à
et
premier à
: on va utiliser là encore le fait que
. Pour cela, comme
et
sont premiers entre eux, on calcule l'identité de Bezout associée :
On aet on a résolu l'équation.
Exercice
Équation multiplicative
Exercice
Équation multiplicative II
Équation diophantienne linéaire à 3 inconnues
Soient , , et quatre entiers. On désire résoudre l'équation-
Étape 1: se ramener au cas où
sont premiers entre eux :
ExplicationOn commence par calculer le pgcd des entiers . L'équation a une solution si et seulement si divise . Dans ce cas, on peut diviser tous les coefficients par cet entier, ce qui nous ramène au cas où ce pgcd est 1. -
Étape 2 :Lorsque
,
,
sont premiers entre eux, on se ramène
au cas où deux des coefficients sont premiers entre eux :
ExplicationSoit le pgcd de et . On pose , avec et premiers entre eux.
Si est une solution de l'équation, on aComme et sont premiers entre eux, il existe un entier tel que et la congruence est équivalente à .Ainsi, si on choisit un représentant de , on aetavec .
.Ainsi, si on choisit un représentant de , on aetavec .
On pose avec . L'équation devientc'est-à-direavec maintenant et premiers entre eux. - Étape 3 : Supposons et premiers entre eux. On cherche (et trouve) une solution particulière avec , ce qui revient à résoudre l'équation :
-
Étape 4 : Supposons
et
premiers entre eux.
On cherche les solutions de l'équation
.
ExplicationL'équation est équivalente àLa discussion dans le cas de deux variables (en considérant comme fixé) implique que si et sont des entiers tels que , et s'écrivent sous la formec'est-à-dire matriciellement -
Étape 5 :Supposons
et
premiers entre eux et
. La solution générale de l'équation
est donnée
de manière matricielle par
avec et appartenant à .
Une équation diophantienne non linéaire sans solution
On désire montrer que
l'équation
n'a pas de solutions entières.
- Soit
un
nombre premier impair. Montrer que si l'équation
a une solution, alors
est congru à
.
Solution - Supposons qu'il existe des entiers et tels que .
- Conclure.
SolutionSoit des entiers et tels que . On a trouvé un nombre premier divisant et congru à 3 mod 4. Pour ce nombre premier,.Donc est un carré modulo , ce qui est absurde, car est congru à .
Pour aller plus loin
Thèmes
- Exercices sur les systèmes linéaires modulaires
- I
- II
- III
- Exercices sur les racines de l'unité dans
- I
- II
- III
- Exercice sur la racine d'un polynôme : Relèvement
- Exercices sur l'authentification : Authentification
- Exercices sur l'identité de Bezout
- I
- II
- III
- IV
- Exercices sur les critères de divisibilité
- I
- II
- III
-
Algorithme d'exponentiation
- Nombre de multiplications
- Exercice sur l'exponentiation
- Exercices sur le logarithme discret
- Log discret I
- Log discret I
- Factorisation par la méthode de Pollard
- Exercices sur les méthodes de cryptologie
- RSA I
- RSA analyse
- RSA création
- RSA décryptage
- Diffie-Hellman I
- Diffie-Hellman II